1. Определённый и неопределённый интегралы. Чем отличаются, связь между ними?

Определенный и неопределенный интеграл является аналогом суммы последовательности. У определенного интеграла есть пределы интегрирования, то есть заданы начальная и конечная точки интегрирования. Поэтому определенный интеграл — это число. У неопределенного интеграла пределы интегрирования не заданы, и такой интеграл будет не числом, а функцией.

2. Множество всех первообразных функций f(x) = 1/(sin²x) - x² + x имеет вид:

Функция F(x) может быть найдена с помощью вычисления неопределенного интеграла от производной f(x)

F(x)=∫f(x)dx

Выпишем интеграл, чтобы решить его.

F(x)=∫(1/(sin²(x))) − x² + xdx

Преобразование из 1/(sin²(x)) в cos²x

∫cos²x - x² + xdx

Разложим интеграл на несколько интегралов:

∫cos²(x)dx + ∫-x²dx + ∫xdx

Поскольку − 1 является константой по отношению к x, вынесем − 1 из интеграла.

-ctg(x) + C - ∫x²dx + ∫xdx

По правилу дифференцирования функции, интегралом от x² относительно x является x³/3

-ctg(x) + C - (x³/3 + C) + ∫xdx

По правилу дифференцирования функции, интегралом от x относительно x является x²/2

-ctg(x) + C - (x³/3 + C) + x²/2 + C

Упростим.

-ctgx - x³/3 + x²/2 + C

ответ: 1

3. Интеграл равен:

Преобразование из 1/(sin²x) в cosec²x

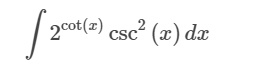
Пусть u = ctgx(x). Тогда du = −cosec²(x)dx, следовательно -du/cosec²(x) = dx

Переписать, используя u и du.

Положим u = ctgx(x).

Найдем du/dx

Дифференцируем ctgx(x)

d/dx[ctgx(x)]

Производная ctgx(x) по x ровна -cosec²(x)

Перепишем задачу с помощью u и du.

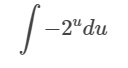
Интеграл 2ᵁ относительно u равен 2ᵁ/(ln(2).

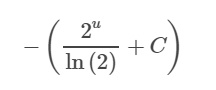
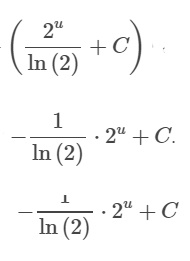
Заменим все u на ctg(x)

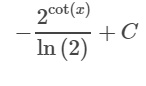
ответ: 2