Построить и исследовать пять квадратичных функций
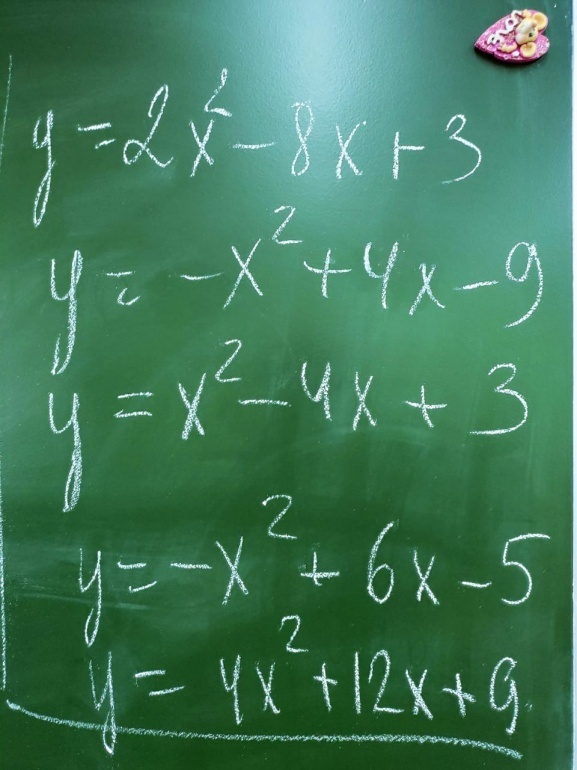
y = 2x² - 8x + 3
y = -x² + 4x - 9
y = x² - 4x + 3
y = -x² + 6x - 5
y = 4x² + 12x + 9
Строим графики - это всё параболы.
Если «a > 0», то ветви направлены вверх.
Если «a < 0», то ветви направлены вниз.
a - это первое число
В каждой функции надо найти три точки: подставим 0 заместо y - найдем 2 точки и третья точка найдем формулой:
x₀ = −b/2a
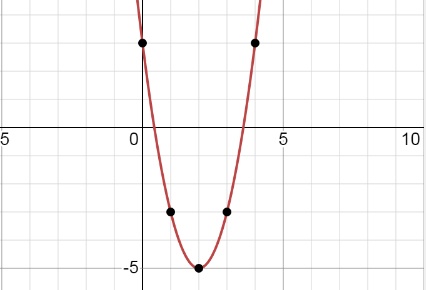
1) y = 2x² - 8x + 3 ветви направлены вверх
x₀ = 8/2*2 = 2
Подставим: y = 2* 2² - 8*2 + 3 = -5
Нулевая точка - вершина (2;-5)
Другие точки:
x 0 4
y 3 3
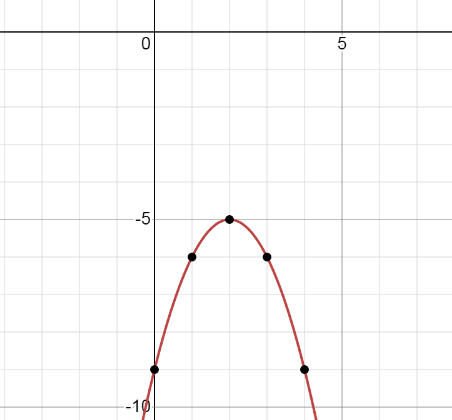
2) y = -x² + 4x - 9 ветви направлены вниз
x₀ = −b/2a
x₀ = -4/2*(-1) = 2
Подставим: y = -2² + 4*2 - 9 = -5
Нулевая точка - вершина (2;-5)
Другие точки:
x 0 4
y -9 -9
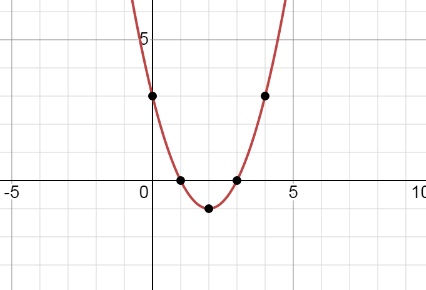
3) y = x² - 4x + 3 ветви направлены вверх
x₀ = 4/2 = 2
Подставим: y = 4 - 4*2 + 3 = -1
Нулевая точка - вершина (2;-1)
Другие точки:
x 0 1 3 4
y 3 0 0 3
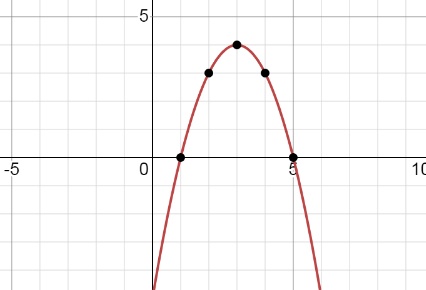
4) y = -x² + 6x - 5 ветви направлены вниз
x₀ = -6/2*(-1) = 3
Подставим: y = -3² + 6*3 - 5 = 4
Нулевая точка - вершина (3;4)
Другие точки:
x 1 2 3 4 5
y 0 3 4 3 0
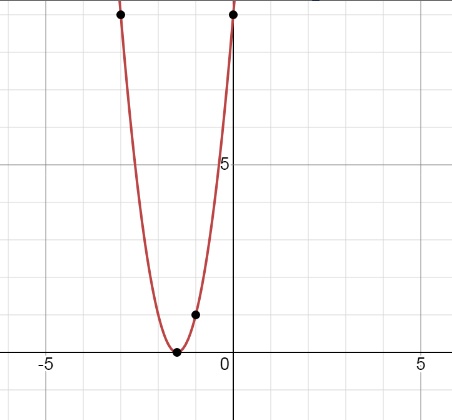
5) y = 4x² + 12x + 9 ветви направлены вверх
x₀ = -12/2*4 = -3/2
Подставим: y = 4*(-3/2)² + 12*3/2 + 9 = 0
Нулевая точка - вершина (-3/2;0)
Другие точки:
x -3 0
y 9 9


 ...
...
 ...
... ...
... ...
...