Геометрия. Задача 1. Высоты, проведенные к боковым сторонам АВ и АС остроугольного равнобедренного треугольника ABC, пересекаются в точке М. Найдите углы треугольника, если ∠BMC= 100°

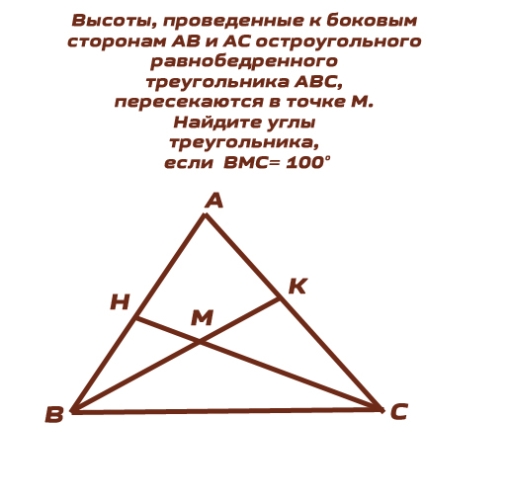
ΔABC - равнобедренный

AB = AC

CH ⊥ AB

BK ⊥ AC

∠BHC=90°

∠BKC=90°

∠BMC=100°

1) Докажем, что ΔBHC = ΔBKC

треугольники ровны, так как

∠HBC = ∠KCB (в равнобедренном треугольнике углы при основании равны)

∠BHC= ∠CKB

соответственно

∠HCB = ∠KBC

BC - общая сторона (гипотенуза)

2) так как ∠HCB = ∠KBC

∠MBC = (180° - 100°) / 2 = 40°

∠ABC = 180° - 40° - 90° = 50°

в равнобедренном треугольнике углы при основании равны

∠ABC = ∠BCA = 50°

∠BAC = 180° - (50° + 50°) = 80°

Ответ: ∠ABC = 50°, ∠BCA = 50°, ∠BAC = 80°