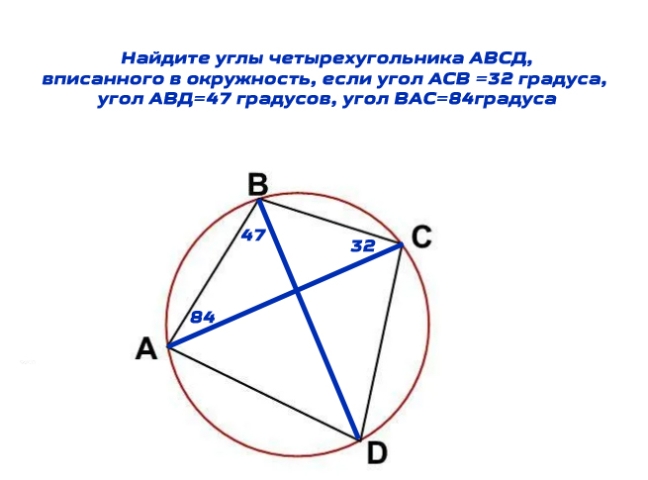
Найдите углы четырехугольника АВСД, вписанного в окружность, если угол АСВ =32 градуса, угол АВД=47 градусов, угол ВАС=84градуса

∠DBC = 180° - ∠BAC - ∠ACB - ∠ABD

∠DBC = 180° - 84° - 47° - 32° = 17°

∠ABC = ∠ABD + ∠DBC

∠ABC = 47° + 17° = 64°

По теореме, сумма противоположных углов вписанного четырехугольника равна 180°, найдем ∠ADC

∠ADC = 180° - ∠ABC

∠ADC = 180° - 64° = 116°

Вписанные углы, опирающиеся на одну и ту же дугу, равны.

∠ABD = ∠ACD

∠BCD = 47 + 32 = 79°

∠BAD = 180° - 79° = 101°

Ответ: ∠BAD = 101, ∠BCD = 79°, ∠ADC = 116°, ∠ABC = 64°