Цель: Закрепление теоретического материала. Научиться определять равнодействующую, уметь применять и решать задачи на равновесие в геометрической форме Уметь анализировать правильность решения
Задание: Определить реакции стержней, удерживающих груз весом G. Массой стержней пренебречь. Схему своего варианта смотри на рисунке 1. Числовые данные своего варианта взять из таблицы
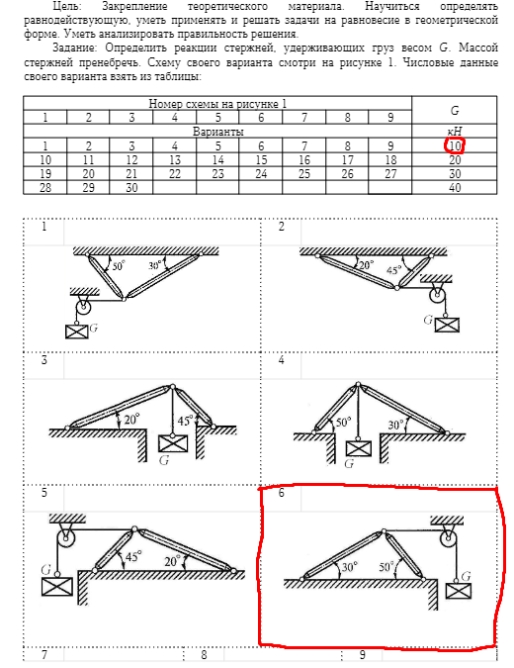

Определение горизонтальных и вертикальных компонент:
Горизонтальная компонента веса груза: F = 10 кН * sin(30°) = 5 кН * √3 / 2 ≈ 8.66 кН
Вертикальная компонента веса груза: F = 10 кН * cos(30°) = 10 кН * 1/2 = 5 кН
Горизонтальная составляющая реакции стержня 1: R = -F = -8.66 кН (направо)
Вертикальная составляющая реакции стержня 1: R = 0 (поскольку вертикальная компонента веса груза компенсируется нитью)
Рассмотрим второй стержень (под углом 50°):
Горизонтальная составляющая реакции стержня 2: R2 = F = 8.66 кН (налево)
Вертикальная составляющая реакции стержня 2: R2 = 0 (поскольку вертикальная компонента веса груза также компенсируется нитью)
Теперь учтем катушку, к которой прикреплена нить:
Горизонтальная компонента натяжения нити: T = R2 - R1 = 8.66 кН - (-8.66 кН) = 17.32 кН (направо)
Вертикальная компонента натяжения нити: T = F = 5 кН (вверх)
На стержень, который прикреплен к нити, действует равнодействующая сила натяжения:
R = √(T^2 + T^2) = √(17.32 кН^2 + 5 кН^2) ≈ 18.1 кН
Угол между натяженной нитью и горизонтом:
θ = arctan(T / T) = arctan(5 кН / 17.32 кН) ≈ 16.18°
реакция стержней составляет около 18.1 кН

Но нужно проверить!

Другие вопросы в разделе - Другое


1 Составьте родословную семьи по короткопалости и определите характер ...

