Помогите пожалуйста, как можно скорее.
1. Найдите область определения функции: y = lg(x² - 3x - 4)
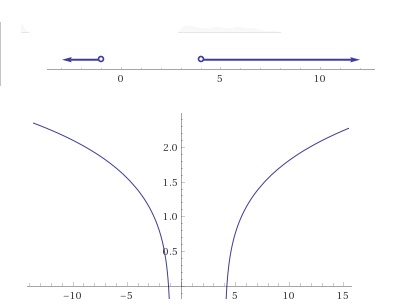
x ∈ R : x < -1 или x > 4}
2. Даны комплексные числа: z₁ = 2 + 3i, z₂ = 5 - 7i
а) z₁ + z₂
2 + 3i + 5 -7i = (2 + 5) + (3 - 7)i = 7 - 4i
б) z₁ - z₂
2 + 3i - (5 - 7i) = (2 - 5) + (3 + 7)i = -3 + 10i
в) z₁ * z₂
(2 + 3i) · (5 - 7i) = 2·5 - 2·7i + 3·5i - 3·7i2 = 10 - 14i + 15i + 21 = 31 + 1i
г) z₁ / z₂
(2 + 3i)/(5 - 7i) = (2*5 + 3(-7))/(5² - 7²) + ((5*3 - 2*(-7))/(5² - 7²))i = (10 - 21)/(25 + 49) + ((15 -14)/(25 + 49))i = -(11/74) + (29/74)i
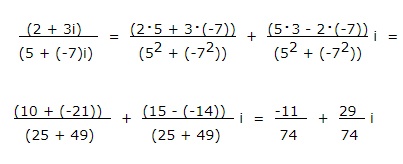
3. Решите уравнение:
5(1/2)^x-3 + (1/2)^x+1= 162
Сделаем замену:
v = (1/2)^x
81v/2 - 162 = 0
81v/2 = 162
v = 4
Делаем обратную замену:
(1/2)^x = v
x = log(v)/log(2)
x₁ = log(4)/log(1/2) = -2
4. Решите уравнение: 4cos²x - 8cosx + 3 = 0
(2cosx - 3)(2cosx - 1) = 0
(2cosx - 3) = 0 или (2cosx - 1) = 0
2cosx = 3 или 2cosx = 1
cosx = 3/2 или cosx = 1/2
x₁ = Пи/3
x₂ = 5Пи/3
5. Найдите наибольшее и наименьшее значение функции:
y = x⁴ - 8x² - 9 на промежутке [0;3]
Находим первую производную функции:
y = 4x³ - 16x
или
y = 4x(x² - 4)
Приравниваем ее к нулю:
4x³ - 16x = 0
fx = 4x(x - 2)(x + 2)
x1 = 0
x2 = 2
x3 = -2
Вычисляем значения функции на концах отрезка
f(0) = -9
f(2) = -25
f(-2) = -25
Ответ: fmin = -25, fmax = 0
6. Вычислите площадь фигуры ограниченную линиями:
y = 2 - x³,
y = 1,
x = -1,
x = 1
Сделаем так:
y = 2 - x³ y = 1
-1 ≤ x ≤ 1
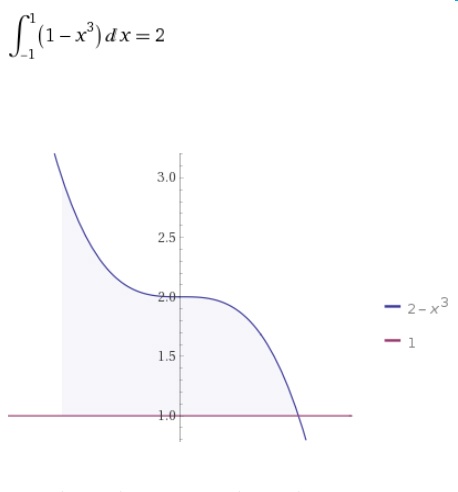
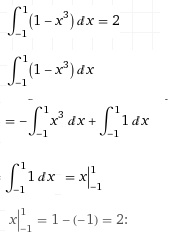
x = 2
7. Составить уравнение касательной и нормали к графику функции:
y = x² - 3 в точке c с абсциссой x₀ = 2
Запишем уравнения касательной в общем виде:
yk = y₀ + y(x₀)(x - x₀)
По условию задачи x₀ = 2, тогда y₀ = 1
Теперь найдем производную:
y = (x²-3) = 2x
следовательно:
f(2) = 2 * 2 = 4
В результате имеем:
yk = y₀ + y(x₀)(x - x₀)
yk = 1+4(x - 2)
или
yk = 4x - 7
Запишем уравнения нормали в общем виде:
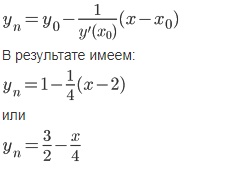

Другие вопросы в разделе - Математика

Найдите наибольшее и наименьшее значения функции f(x) = −x^3− ...



 помогите решить контрольную ...
помогите решить контрольную ...