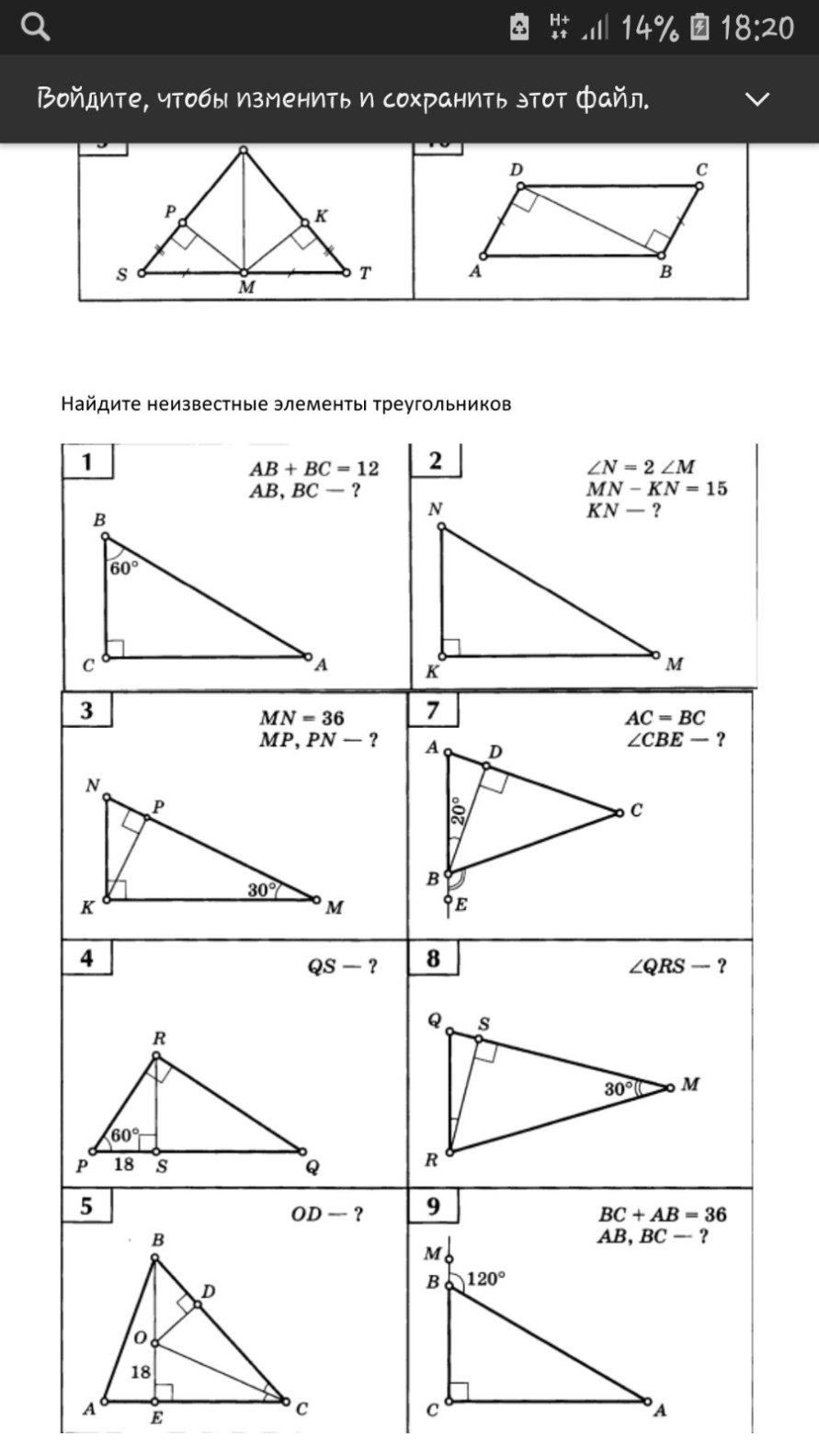
1. Дано: Треугольник ABC
∠B = 60°
∠C= 90°
AB + BC = 12
AB = ?
BC = ?
2. Дано: Треугольник KNM
∠K= 90°
∠N= 2 ∠M
MN - KN = 15
KN = ?
3. Дано: Треугольник KNM
∠K= 90°
∠M= 90°
Точка P делит MN на два отрезка
∠KPN = 90°
MN = 36
MP = ?
PN = ?
4. Дано: Треугольник PRQ
∠K= 90°
∠M= 90°
Точка S делит PQ на два отрезка
∠PSR = 90°
∠P = 60°
PS = 18
QS = ?

1) ∠А=30

в прямоугольном треугольнике катет, лежащий напротив угла в 30 градусов = 1/2 гипотенузы.

если BC = x, то гипотенуза AB = 2x

2x+x = 12

x = 4

Ответ: BC = 4, AB=8

2) Сумма острых углов прямоугольного треугольника 90°

Угол N = 2 * ∠M

∠M + 2 *∠M = 3 *∠M

3 * ∠M = 90°

∠M = 30°

KN лежит против угла = 30° и равен половине гипотенузы MN (свойство)

MN = 2KN

2KN - KN = 15 см

KM = 15 + 15 = 30 см

Ответ: KM = 30 см

3) △MNK (угол K=90 градусов)

угол M = 30°

следовательно NK=1/2 NM (по свойству прямоугольных триугольников) = 18 см.

∠M = 30°

90° - 30° = 60° = ∠N

△NKP (угол P=90 градусов)

∠N=60°

90° - 60° = 30° = ∠ NKP

∠NKP =30°

NP = 1/2 NK = 9 см

MN = MP+PN

PM = NM - NP = 36 - 9 = 27 см

Ответ: NP = 9 см, MP = 27 см

4) В прямоугольном треугольнике сумма острых углов равна 90°. Катет лежащий напротив угла в 30° равен половине гипотенузы.

В ΔPSR (∠PSR=90°): ∠SPR=60° ⇒ ∠SRP = 90°-60° = 30°

PS - катет лежащий напротив ∠SRP=30°, поэтому PR = 2·PS = 2·18 = 36 см.

В ΔPRQ (∠PRQ=90°): ∠RPQ=60° ⇒ ∠RQP = 90°-60° = 30°

PR - катет лежащий напротив ∠RQP=30°, поэтому PQ = 2·PR = 2·36 = 72 см.

SQ = PQ-PS = 72-18 = 54 см

Ответ: 54 см.