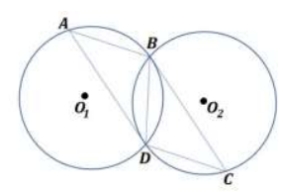
Прямые BC и AD –
касательные к окружностям с
центрами 01 и 02 соответственно
(рис.2). Докажите, что:
1) AB||DC;
2) BD2 = AB ∙ CD

o1;o2¦>ABDC¬o1;o2

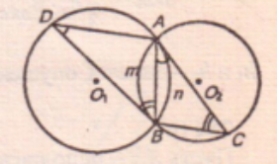
m и n - хорды

так как ∠DBA и ∠CAB - углы между касательными и хордами

∠DBA = 1/2⌒AmB = ∠BCA

∠CAB= 1/2⌒AnB = ∠ADB

Далее:

∠DAB = 180° - ∠ADB - ∠DBA = ∠ABC

Соответственно:

AD параллельна BC, так как ∠DAB=∠ABC как накрест лежащие углы