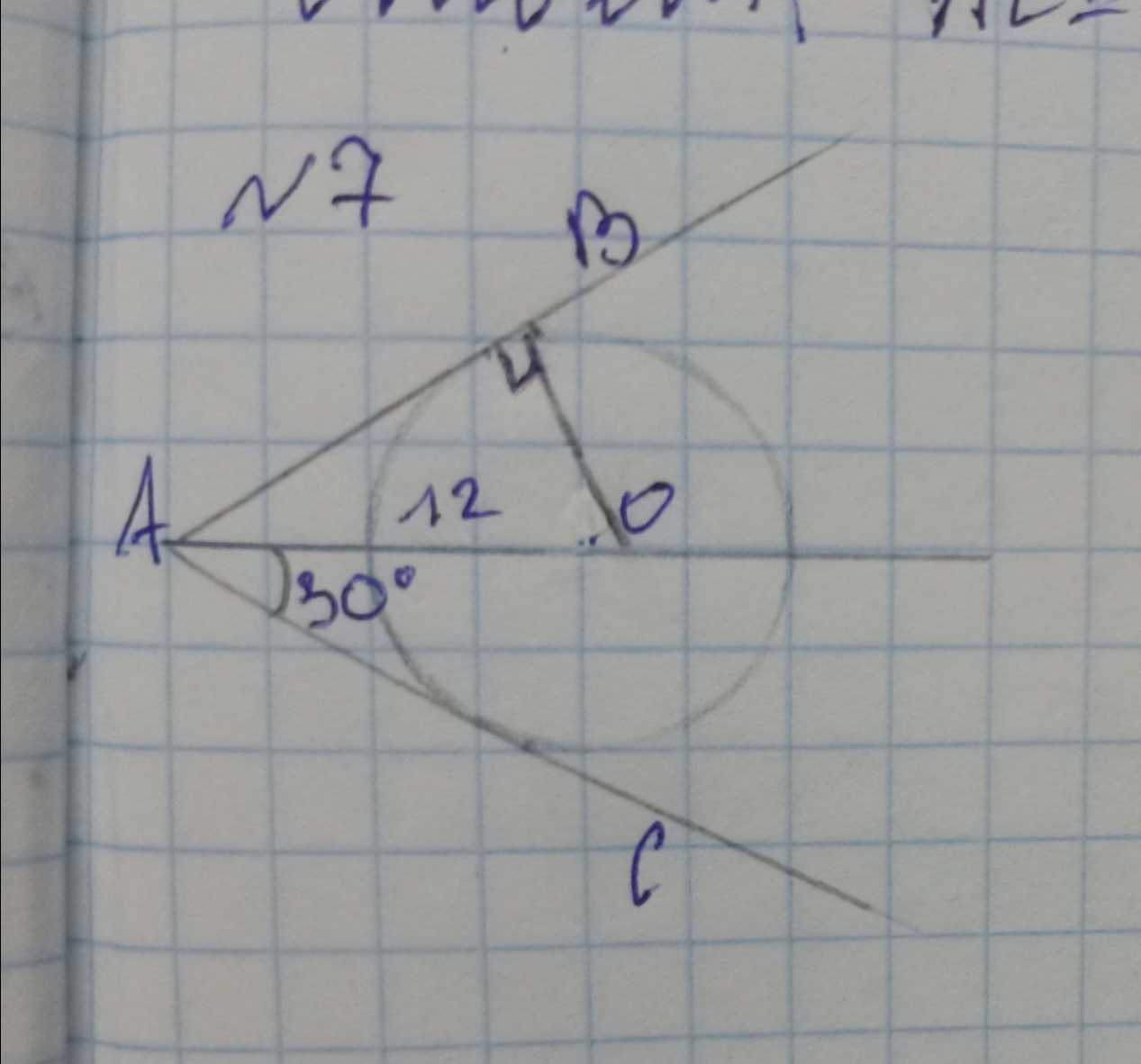
AB и AC - отрезки касательных. AO=12 см, угол ОА=30°. Найти Ас и радиус окружности

1) Проведём из центра окружности линию к точке касания C

2) Прямая проведённая из центра окружности к касательной- перпендикулярна ей

3) Значит ∠ACO = 90°

4) рассмотрим ΔAOC - прямоугольный

АО - гипотенуза

OC - его катет и радиус окружности

По правилу: катет лежащий против угла 30° равен половине гипотенузы

Значит:

OC = 1/2 * АО = 1/2 ° 12 = 6 см

Радиус окружности: 6 см

5) Теперь найдем катет AC

по теореме Пифагора: квадрат длины гипотенузы равен сумме квадратов длин катетов

AO² = AC² + CO²

AC² = AO² - CO²

AC² = 12² - 6² = 108

AC = √108 = 6√3

Ответ: Радиус окружности: 6 см. AC = 6√3