Помогите пожалуйста ещё надо решить
2. Найдите неизвестную сторону треугольника DEF, если DE = 4 см DF= 2 см, угол D равен 30°.
Ответ: ____________ Сделать рисунок.
3. В треугольнике ABC, если AB = 7 см, угол B равен 30°, угол C равен 45°. Найдите сторону AC.
Ответ: ________________ Сделать рисунок.

4. Найдите радиус круга, площадь которого равна 9π см3.
Ответ: __________________

5. Длина дуги окружности равна 2π см. Найдите градусную меру этой дуги, если радиус окружности равен 30 см.
Ответ: _________________

6. Найдите площадь кругового сектора, если угол сектора равен 120°, а радиус круга равен 9 см. В ответе укажите площадь, делённую на π.
Ответ: _________________
Найдите все углы правильного восемнадцатиугольника.
Ответ: _________________

7. Какие координаты имеет середина отрезка AB, если A (2; - 7),
B (6; -3).
1) (2; -2) 2) (4; -5) 3) (8; -10) 4) (-4; 5)
Ответ: ________________

8. Найдите расстояние между точками C и D, если C (-1; 2), D (-7; 10).
Ответ: ___________________

9. Каждой из окружностей укажите координаты её центра и радиус.
A) x2 +(y -1)2 =1
Б) (x – 1)2 +y2 =1
В) x2 +y 2 =1
Г) (x – 1)2 +(y -1)2 =1
Подсказка: в 1 и 2 теоремы косинусов и синусов. Записывайте формулы, которые использовали. Обязательно записывайте ответы.

2. Дано:

△DEF

DE = 4

DF = 2 (проверь это значение, такое оно в задании или нет)

∠D = 30°

FE = ?

Решение:

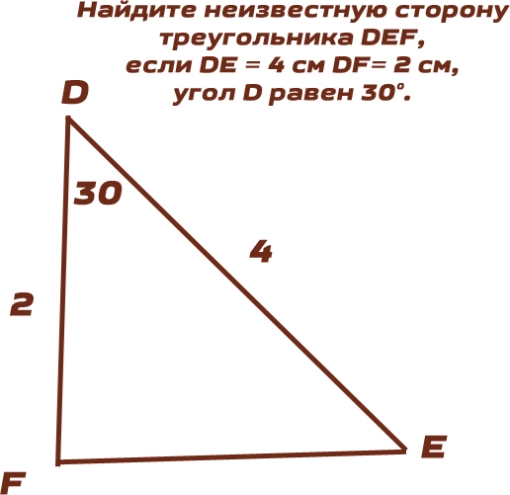
По теореме косинусов

FE² = DE² + DF² - 2 * DE * DF * cos30

FE² = 16 + 4 - 2 * 4 * 2 * √3\\2 = 20 - 16 * √3\\2 = 20 - 8√3

EF=√4=2 см.

EF = √(20 - 8√3)

3. Дано:

△ABC

AB = 7

∠B = 30°

∠C = 30°

AC = ?

Решение:

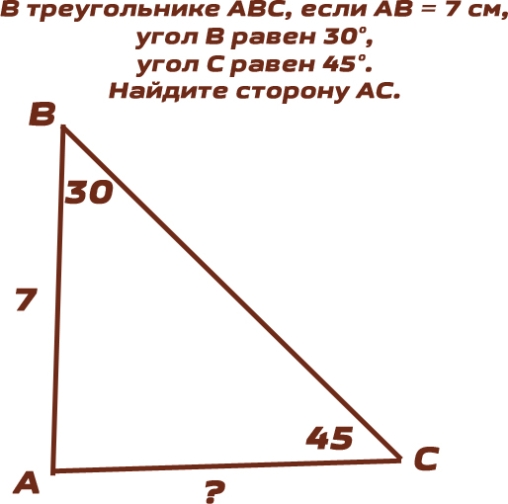
В треугольнике, теорема синусов гласит:

a/sinA = b/sinB = c/sinC

где a, b, и c - стороны треугольника, а A, B, и C - соответствующие им углы.

В вашем случае, у нас есть сторона AB = 7 см, угол B = 30° и угол C = 45°. Нам нужно найти сторону AC.

Сначала найдем угол A. Поскольку сумма углов в треугольнике равна 180°, то A = 180° - B - C = 180° - 30° - 45° = 105°.

Теперь мы можем использовать теорему синусов, чтобы найти AC:

AC/sinA = AB/sinB

AC = AB * sinA/sinB

AC = 7 * sin105°/sin30°

AC = 7 * √3/2 / 0.5

AC = 7 * √3 см

4. Площадь круга определяется формулой:

A = πr²

где A - это площадь круга, r - это радиус круга.

В вашем случае, площадь круга равна 9π см². Подставим это значение в формулу и решим уравнение относительно r:

9π = πr²

r² = 9

r = √9

r = 3 см

5. Длина дуги окружности определяется формулой:

L = r * θ

где L - длина дуги, r - радиус окружности, а θ - градусная мера угла в радианах, которая соответствует данной дуге.

В вашем случае длина дуги L = 2π см, а радиус r = 30 см. Подставим эти значения в формулу и решим уравнение относительно θ:

2π = 30 * θ

θ = 2π / 30

θ = π / 15 радиан.

Если вы хотите перевести радианы в градусы, используйте формулу:

θ (в градусах) = θ (в радианах) * 180 / π

θ (в градусах) = (π / 15) * 180 / π

θ (в градусах) = 12°

Градусная мера дуги равна 12°

6. Площадь кругового сектора определяется формулой:

A = 0.5 * r² * θ

где A - площадь сектора, r - радиус окружности, а θ - градусная мера угла в радианах, которая соответствует данному сектору.

В вашем случае радиус r = 9 см, а угол сектора равен 120°. Для применения формулы нам нужно преобразовать градусы в радианы. Используем формулу:

θ = θ (в градусах) * π / 180

θ = 120 * π / 180

θ = 2π / 3

Теперь подставим эти значения в формулу и найдем площадь сектора:

A = 0.5 * 9² * 2π / 3

A = 27π

Таким образом, площадь сектора равна 27π см²

7. Середина отрезка AB находится в точке, координаты которой равны среднему арифметическому координат концов отрезка. То есть, если A(x1, y1) и B(x2, y2), то середина отрезка M будет иметь координаты M((x1+x2)/2, (y1+y2)/2)

В данном случае, точка A имеет координаты (2, -7), а точка B - (6, -3). Поэтому, координаты середины отрезка AB будут равны:

M = ((2+6)/2, (-7-3)/2)

M = (4, -5).

8. Для нахождения расстояния между двумя точками на плоскости используйте формулу расстояния между точками:

d = √((x2 - x1)² + (y2 - y1)²)

где (x1, y1) и (x2, y2) - координаты точек на плоскости.

В данном случае, точка C имеет координаты (-1, 2), а точка D - (-7, 10). Подставим эти значения в формулу:

d = √((-7 - (-1))² + (10 - 2)²)

d = √((6)² + (8)²)

d = √(36 + 64)

d = √100

d = 10

9. Для того, чтобы найти координаты центра и радиус окружности, нужно привести уравнение окружности к каноническому виду, который выглядит так: (x - a)² + (y - b)² = r², где (a, b) - координаты центра окружности, а r - радиус.

A) x² + (y - 1)² = 1

Координаты центра: (0, 1)

Радиус: 1

Б) (x – 1)² + y² = 1

Координаты центра: (1, 0)

Радиус: 1

В) x² + y² = 1

Координаты центра: (0, 0)

Радиус: 1

Г) (x – 1)² + (y - 1)² = 1

Координаты центра: (1, 1)

Радиус: 1