1) Найдите стороны параллелограмма, зная, что его периметр равен 120 см, а одна из сторон в 3 раз меньше другой.
2) Найдите стороны параллелограмма ABCD, зная что его периметр равен 24 см.
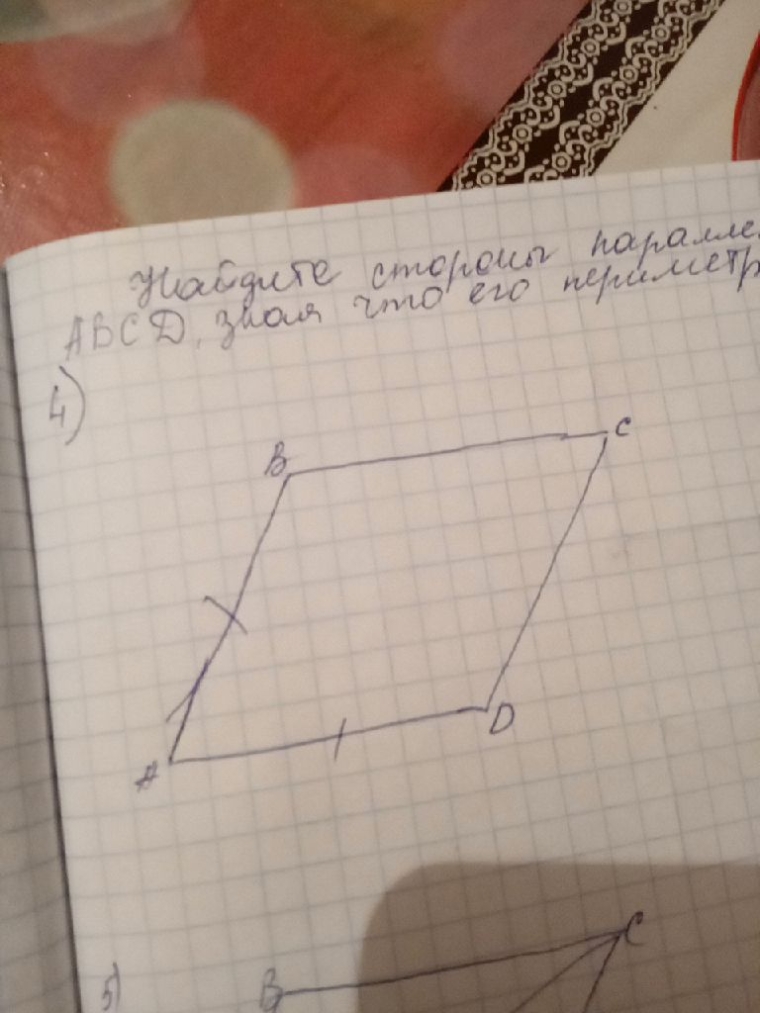

Ответы:
2) Свойства параллелограмма: Противолежащие стороны равны. AB = CD, BC = AD
По условию AB = AD
Значит все стороны ровны.
Зная, что периметр равен 24, найдем все стороны:
24 / 4 = 6
Все стороны параллелограмма ровны по 6 см
1) Периметр параллелограмма высчитывается по формуле:
P = 2(a + b), где a и b стороны параллелограмма
Пусть x - одна сторона
Тогда 3x - вторая
На основе формулы периметра составим уравнение:
2(x + 3x) =120
2 * 4x = 120
8x = 120
x = 15 - длина двух равных сторон
3 * 15 = 45 - длина двух других равных сторон
Проверим: 2(15 + 45) = 120
1
Отв. дан
Creator


Надо под вторым где периметр равен 24 см.
0
Отв. дан
Aleksandra


смотри первый комментарий, там решение
0
Отв. дан
Creator


Спасибо, увидела
0
Отв. дан
Aleksandra


Для написания вопросов и ответов необходимо зарегистрироваться на сайте
Другие вопросы в разделе - Геометрия

d3putatskiy
2023-09-15 12:17:06

Jthgbgn
2023-06-08 05:58:15

Sergei
2023-05-16 07:16:16
Найдите углы четырехугольника АВСД, вписанного в окружность, если угол ...

Sergei
2023-05-16 07:08:16